What is Heap Data Structure? Types and Applications

Published: 04 Apr 2025

Heap Data Structure

A particular type of binary tree called a heap data structure is used to efficiently handle data, particularly for activities like sorting and priority queues. Ever wondered why some tasks get picked before others in a to-do list app? That’s the magic of heaps! Many beginners struggle to understand heaps because of their tree-like shape and array storage—confusing, right? Imagine trying to organize tasks by importance—heaps help computers do just that, and it’s simpler than it sounds once you get the hang of it.

Table of Content

Heap Data Structure
A heap data structure: what is it?
Heap Data Structure Types
1. Min Heap
2. Max Heap
Heap Operations Explained
Heap Implementation
Applications of Heap
Benefits and Drawbacks of Heap Data Structures
1. Advantages
2. Disadvantages
Conclusion About Data Structure Heap
FAQS Min Heap

A heap data structure: what is it?

A heap data structure is a particular kind of binary tree in which the order of each parent node’s children is predetermined. The father of a min heap is always smaller than its offspring. The parent is always larger in a max heap. Since heaps are entire binary trees, there are no gaps between any of the layers from left to right.

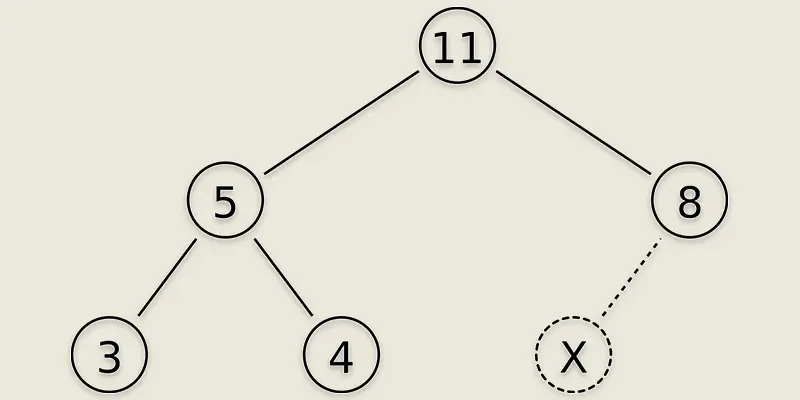
Heap Data Structure Types

Based on how they store data, heaps can be divided into two primary categories

Min Heap

The root (top) always has the smallest value.
All parent nodes are smaller than their offspring.
Used when you need quick access to the minimum value.
Example: In a to-do list, the task with the earliest deadline comes first.

Max Heap

At the root, the greatest value is always found.
Each parent node is superior to its offspring.
Used when you need quick access to the maximum value.
Example: In a game leaderboard, the top scorer stays at the top.

Heap Operations Explained

Heaps support a few basic operations that help manage and organize data. Here are the main ones

Insertion

What it does: Adds a new element to the heap.
How it works: Place the element at the end, then move it up (heapify up) to keep the heap rule.
Example: In a Min Heap, if you insert 2, it moves up to the top if it’s the smallest.

Tip: Think of bubbles in water—smallest bubbles rise to the top!

Deletion (Remove Root)

What it does: Removes the top (root) element.
How it works: Replace the root with the last element, then move it down (heapify down) to fix the heap.
Example: In a Max Heap, removing 100 puts a smaller number on top temporarily, but it will move down.

Analogy: Imagine removing the king from a throne—someone else must rise, and order needs to be restored!

Peek (Get Min or Max)

What it does: Returns the root without removing it.
How it works: Just look at the first element in the array or tree.
Example: In a Min Heap, peek gives you the smallest number.

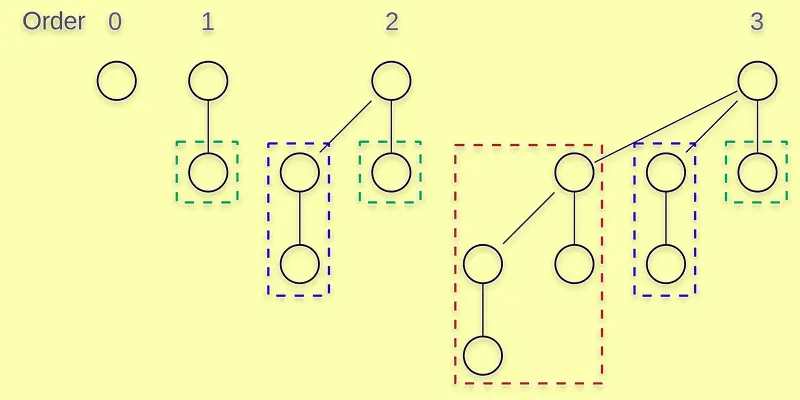
Heap Implementation

Heaps are special trees that organize data based on size. Min-heaps place smaller values above larger ones, and max-heaps do the opposite.Arrays are commonly used to create heaps for effective access and storage. Operations like insertion and deletion are performed in logarithmic time (O(log n)), making heaps efficient for priority queue operations.

Example

If you have a max-heap storing integers [10, 5, 3, 2], the largest value (10) will always be at the root. If you add a new element, say 7, it will be placed at the appropriate position to maintain the heap property.

Applications of Heap

Because heaps are effective at preserving a partially sorted structure, they are frequently employed in a variety of computer science applications.Their ability to quickly access the largest or smallest element makes them ideal for priority queues, sorting algorithms, and more.

Priority Lines: The element with the highest or lowest priority can be efficiently retrieved and removed thanks to heaps.
Heap Sort: Heaps can be used to build an efficient sorting algorithm with a temporal complexity of O(n log n).
Graph Algorithms:Algorithms such as Dijkstra’s shortest path employ heaps to extract minimal values efficiently.
Maintenance of the Median: In a stream of numbers, heaps can be used to track the median.
Memory Management: Heaps are used in dynamic memory allocation to manage memory blocks.
Scheduling Algorithms: Heaps help in scheduling tasks based on priority in systems like CPU scheduling.

Benefits and Drawbacks of Heap Data Structures

The heap data structure is renowned for its effectiveness in managing activities based on priorities and preserving a structure that is partially sorted. While heaps offer fast access to the largest or smallest elements, they do come with some limitations.

Advantages

Efficient for priority queue operations.
Fast insertion and deletion (O(log n)).
Can be implemented using arrays, saving space.
beneficial for heap sort implementation (O(n log n) time complexity).

Disadvantages

Not suitable for searching elements in arbitrary positions (O(n) time).
Operations like insertion and deletion require restructuring, which can be costly in some cases.
Heaps are not fully sorted, just partially.
Complexity increases when dealing with large datasets.

Conclusion About Data Structure Heap

We’ve covered the Heap Data Structure in detail. From its efficient use in priority queues to its role in graph algorithms and sorting, heaps are a valuable tool in computer science. I highly recommend learning heaps, as they can significantly improve your problem-solving skills in many programming challenges. If you’re interested in mastering heaps or other data structures, dive deeper into the topic and explore more examples. Don’t forget to share your thoughts or questions in the comments below!

FAQS Min Heap

Is heap a data structure?

A heap is indeed a specific type of tree-based data structure. Depending on whether it’s a max-heap or min-heap, it keeps the parent and child nodes in a certain sequence, with each parent being either larger or smaller than its offspring. Sorting algorithms and priority queues are frequently implemented using heaps.

When to use heap data structure?

You should use a heap when you need efficient access to the highest or lowest value in a dataset, like in priority queues. It’s ideal for situations where frequent insertion and removal of elements are required. Examples include scheduling tasks or finding the shortest path in graph algorithms.

Complexity of heap data structures with time

For insertion, deletion, and heapifying, the temporal complexity of heap operations is typically O(log n). Accessing the maximum or minimum element is O(1). However, searching for an arbitrary element is O(n) since heaps are not fully sorted.

Which data structure to use?

The choice of data structure depends on your needs. Use heaps when you need efficient priority-based operations, linked lists for dynamic data with frequent insertions/deletions, and arrays for fast indexed access. For balanced search operations, trees like binary search trees or hash tables are more suitable.